Nas Máquinas de Turing Paraconsistentes (MTPs) cada função de escolha de valores dos diferentes elementos da máquina, representa uma configuração de uma Máquina de Turing Clássica (MT). Portanto, a configuração das MTPs podem ser interpretadas como uma superposição de configurações de uma MT além de, no final da computação, ser realizada só uma escolha de valores dos elementos da máquina para obter um único resultado. As MTPs podem ser consideradas similares as Máquinas de Turing Quânticas (MTQs) nas quais são permitidas somente superposições uniformes.
 Emaranhamento Quântico
Emaranhamento Quântico
Contudo, não é possível representar estados emaranhados nas MTPs através da mera interpretação da multiplicidade de valores como superposição de estados. Isso porque qualquer superposição uniforme emaranhada de estados exclui alguma combinação de valores dos elementos constituintes, enquanto, nas MTPs, qualquer combinação de valores na configuração da máquina pode ser obtida, ou seja, nenhuma combinação é excluída.
A noção de fase relativa nas MTQs também não é diretamente representável através das MTPs, e essa característica é essencial para a interferência quântica, que é o mecanismo provido pelas MTQs para aproveitar o paralelismo no processo de computação. O mecanismo provido pelas MTPs para aproveitar o paralelismo e bastante diferente da interferência quântica: consiste na adição de condições de inconsistência na definição das instruções.
 Interferência QuânticaLeia mais »
Interferência QuânticaLeia mais »


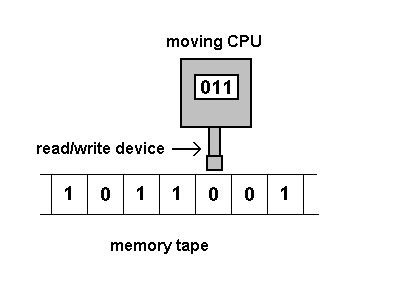 Em uma máquina de Turing Quântica, ler, escrever e trocar de operações são todas funções realizados via interações quânticas. A fita e a cabeça em si existem em um estado quântico. No lugar da célula de Turing na fita clássica, que pode abrigar apenas bits 0 ou 1, a máquina de Turing Quântica abriga Qubits, que apresentam estados de superposição de 0 ou 1. Uma máquina de Turing Quântica pode codificar muitas entradas para um problema simultaneamente, e então calcular todas as entradas ao mesmo tempo.
Em uma máquina de Turing Quântica, ler, escrever e trocar de operações são todas funções realizados via interações quânticas. A fita e a cabeça em si existem em um estado quântico. No lugar da célula de Turing na fita clássica, que pode abrigar apenas bits 0 ou 1, a máquina de Turing Quântica abriga Qubits, que apresentam estados de superposição de 0 ou 1. Uma máquina de Turing Quântica pode codificar muitas entradas para um problema simultaneamente, e então calcular todas as entradas ao mesmo tempo.


 Alan Turing
Alan Turing

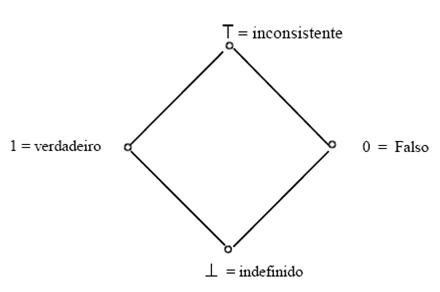 Reticulado Finito
Reticulado Finito
 Newton da Costa e Família
Newton da Costa e Família Formatura de Newton da Costa em engenharia civil (1952)
Formatura de Newton da Costa em engenharia civil (1952)



