Um resumo sobre a computação quântica!

A internet é mesmo incrível. Eis que fizeram o vídeo mais incrível com um resumo completo do que compõe a computação quântica.

Simplesmente assistam este incrível vídeo que possuí uma quantidade incrível de informações em apenas 7 minutos!

Lógica Paraconsistente: Máquina de Turing Paraconsistente Não Separáveis

As Máquina de Turing Paraconsistente Não Separáveis (MTPNSs) permitem a mistura de caminhos indiscriminadamente não permitindo aproveitar de forma adequada o paralelismo. Isso ocorre porque todas as possíveis combinações de estados e símbolos nas células da fita são considerados na execução das instruções. Essa é uma característica de algumas propriedades da LFI1 como a conjunção que valida a regra de separação (se ├LFI1 A^B então ├LFI1 A e ├LFI1 B) e a regra de adjunção (se ├LFI1 A e ├LFI1 B então ├LFI1 A^B). Assim, se Δ_LFI1 (M(n)) ├ Qi(t, x) ^ Sj(t, x) e Δ_LFI1 (M(n)) ├  Qk(t, x) ^ Sl(t, x), é também possível deduzir Δ_LFI1 (M(n)) ├ Qi(t, x) ^ Sl(t, x) Δ_LFI1 (M(n)) ├ Qk(t, x) ^ Sj(t, x). Consequentemente, se quiser definir um modelo de MTPs onde os diferentes caminhos de computação não se misturem totalmente, deve-se considerar uma lógica paraconsistente onde não seja valida a regra de separação ou a regra de adjunção (ou ambas).

Existem lógicas paraconsistentes com conjunções não-adjuntivas, como a lógica discursiva de primeira ordem D2. Para utilizá-la novos axiomas teriam que ser propostos para indicar quando diferentes elementos no processo de computação podem ser considerados em conjunto. Como não existem lógicas paraconsistentes onde a regra de separação não seja válida, é preferível definir uma lógica paraconsistente na qual não seja valida a regra de separação, de forma a permitir interpretar os diferentes elementos da máquina correspondentes a um caminho de computação como estando inter-relacionados, o que permitirá pensar em caminhos de computação independentes.

Uma lógica paraconsistente não-separável (PNS5) é obtida a partir da lógica modal S5 através da função de tradução do conjunto de fórmulas ForPNS5 → ForS5. Dessa maneira a lógica PNS5 fica definida e é uma sublógica de S5. A definição dos conectivos em PNS5 são:

• O conectivo • de inconsistência: •A = A ^◊ ￢◊A = ◊A ^ ◊￢A, em S5;
• O conectivo ◦ de consistência: ◦A = ￢◊•A = □￢A v □A em S5;
• A negação clássica ￢: ￢A = ￢◊A ^◊ ◦A = ◊￢A ^ (□￢A v □A) em S5;
• A conjunção clássica: A^B = (A ^◊ B) ^◊ (◦A ^◊ ◦B) = ◊(A ^ B) ^ (□(A ^ B) v □(A ^ ￢B) v □(￢A ^ B) v □(￢A ^ ￢B)) em S5.

Com estas definições, os princípios de explosão passam a ser teoremas de PNS5. Tendo em conta tais características PNS5 pode legitimamente ser considerada como uma LFI. Para poder usar PNS5 em lugar da LFI1, é necessário estende-la à primeira ordem incluindo os quantificadores e a igualdade, S5Q⁼.

Lógica Paraconsistente: Máquina de Turing Paraconsistente

Nas Máquinas de Turing Paraconsistentes (MTPs) é possível, em principio, usar qualquer lógica paraconsistente de primeira ordem. A versão de primeira ordem utilizada foi a LFI1 lógica de inconsistência formal (LFI) que estende a lógica positiva clássica incluindo conectivos de consistência ◦ e inconsistência •, além de ter uma semântica simples e bem estabelecida.

As noções de inconsistência e contradição coincidem, através da equivalência •A ↔ (A^￢A), e o conectivo de consistência serve para recuperar o caráter explosivo das contradições:

• se Δ |- _LFI1 a e Δ |- _LFI1￢a
• então Δ , ◦α |- _LFI1 β para toda fórmula β.

Além disso, ela permite codificar todas as inferências validas da lógica de primeira ordem clássica.

Pelo fato de LFI1 ser uma extensão da lógica positiva clássica, a aplicação de múltiplas instâncias de esquemas de axiomas do tipo Aij (I), Aij (II) ou Aij (III), para o mesmo instante de tempo t, denota a execução simultânea das respectivas instruções, o que pode levar a multiplicidade de símbolos em algumas células da fita, ou a multiplicidade de estados ou posições da máquina. Tal multiplicidade, em conjunção com o uso de axiomas do tipo (Aqi) ou (Asj), necessariamente leva a contradições, as quais em LFI1 são identificadas com inconsistências.

Adicionando condições de inconsistência nos dois símbolos iniciais das instruções de forma a controlar sua execução, q•i indicará que a instrução será executada unicamente no caso em que a maquina esteja em múltiplos estados ou posições, enquanto s•j indicará que a instrução será executada unicamente no caso em que a célula da fita (onde a instrução vai ser executada) contenha múltiplos símbolos. Estas condições correspondem formalmente a colocar o conectivo •, respectivamente, na frente do predicado Qi ou Sj no antecedente dos axiomas que expressam instruções. Estas condições permitem aproveitar o paralelismo das MTPs.

Lógica Paraconsistente: Máquina de Turing

Para falarmos da máquina de Turing, precisamos conhecer seu criador: Alan Mathison Turing (1912-1954), conhecido também como Alan Turing. Ele foi um matemático britânico nascido em 23 de junho de 1912 na cidade de Paddington, na Inglaterra. Estudou na tradicional Escola Sherbourne tendo-se graduado em 1931 em Matemática pela Universidade de Cambridge.

Alan Turing

Depois de formado, e após muito estudo, criou uma máquina automatizada que calcula qualquer algoritmo e processa as instruções mecanicamente na própria máquina. Essa é a tão famosa Máquina de Turing que serviu como protótipo para os computadores atuais e permitiu o desenvolvimento do “Enigma” que foi capaz de decifrar os códigos nazistas na Segunda Guerra Mundial.

Máquina de Turing

Uma Máquina de Turing pode ser descrita como sendo constituída por uma cabeça de leitura/escrita e uma fita unidimensional potencialmente infinita em ambas as direções. A fita e dividida em células, cada uma das quais com capacidade de conter um único símbolo. Em cada instante de tempo a máquina se encontra em um determinado estado, e com a cabeça lendo uma célula especifica da fita, a qual ela considerada como sendo a posição atual da maquina. A configuração atual da maquina consiste na junção do estado atual e do símbolo que esta sendo lido na posição atual.

O comportamento da máquina é determinado por um conjunto de instruções, as quais indicam a operação a se realizar dependendo da configuração atual. As únicas operações que a maquina pode realizar são: escrever um novo símbolo na posição atual (substituindo o símbolo anterior) ou realizar um movimento da cabeça a esquerda ou direita, passando a uma célula subsequente da atual. Os estados, os símbolos de leitura/escrita e as instruções são conjuntos finitos.

Resenha do livro “Programming the Universe”

O livro Programming The Universe, foi escrito por Seth Lloyd, professor do famoso MIT. Tendo trabalhado com grandes nomes da física como Murray Gell-Mann, Lloyd traz diversas considerações de sua visão da física quântica, e da computação quântica, em seu livro. Disponível na amazon neste link.

A tese principal do livro é que todo o universo pode ser compreendido como um grande computador quântico que computa e gera informação nas interações de suas partículas fundamentais. Para explicar esta tese, Lloyd tenta conceituar em seu livro os diversos fundamentos da computação, da mecânica quântica, da teoria da complexidade, e tenta unir os fundamentos da computação com os da mecânica quântica para tentar explicar um pouco a história do universo, do passando pelo Big Ben, observando o universo como um grande computador quântico.

Lloyd demonstra em seu livro que o universo computa, ou seja, faz computação, registrando e transformando informação em seus movimentos de expansão, através das leis de entropia, que de acordo com o livro: “Se pudermos olhar a matéria na escala atômica, nós poderíamos ver os átomos dançando randomicamente. A energia que dirige essa randomicidade é chamada de entropia. Entropia é a informação requirida para especificar os movimentos randômicos dos átomos e moléculas, movimentos muito pequenos para nós vermos. Entropia é a informação contida em um sistema físico que é invisível a nós”.

Lloyd passa em seus livros sobre os diversos fundamentos quânticos, como a “ação fantasmagórica à distância”, o princípio de incerteza de heisenberg, a dualidade partícula/onda dos elementos quânticos, o emaranhamento, o gato schrodinger, e demais fundamentos quânticos que estamos explorando aqui neste blog.

Esta foi a dica de livro quântico desta vez, aguardem por mais livros em breve!!

A história da computação quântica!

Para desenvolvermos a computação quântica comercial e prática, ainda há um caminho longo a ser percorrido, apesar dos avanços dos últimos anos na área. É válido realizarmos um retrospecto, para entendermos os avanços da computação que nos trouxeram até aqui. Neste post, vamos, desde os primórdios, realizar um resumido retrospecto da computação quântica!

A palavra “calcular” vem do grego e significa “pedra”, mostrando os primórdios das ferramentas de cálculo e computação (“cálculo renal” é sinônimo de “pedra nos rins”). Há mais de 5 mil anos, surgiu o ábaco e diversas outras tecnologias como a “anticítera”, há mais de 2 mil anos atrás. Todas essas tecnologias, porém, apenas realizavam uma tarefa por vez (somar, dividir, multiplicar, etc).

Em 1830, Charles Babbage cria o primeiro computador programável (modelo teórico que utilizava tecnologia mecânica e a vapor).

Em meio a crise da física clássica, no século XX, pesquisadores como Heisenberg e Schrodinger lançam as fundações para aquela que seria conhecida como mecânica quântica. Apesar de matematicamente consistente, a mecânica quântica não está esclarecida e demonstra uma multiplicidade de interpretações teóricas. Essa dificuldade se deve ao fato de a mecânica quântica não ser intuitiva como a mecânica clássica, que se baseia em elementos observáveis.

Em 1931 Godel cria teoremas mostrando as limitações do conhecimento matemático, influenciando a ciência da computação (um exemplo disso é que é impossível fazer um computador encontrar erros de programação de maneira automática). Em computação, dividimos problemas em “tratáveis” e “intratáveis”, com relação a sua solubilidade. Muitos são intratáveis por conta de fatores exponenciais de operações para a sua resolução, o que vem a mudar de panorama com a computação quântica.

Em 1936 Turing e Church criam os modelos teóricos para computadores, fundando a ciência da computação com a máquina de Turing.

Em 1943, os estudos com o ENIAC e o Colossus introduziram a eletrônica na computação. Surgem nesta época os transistores e os circuitos integrados, revolucionando a tecnologia de válvulas dos primeiros computadores.

Em 1948 Claude Shannon em seu livro “uma teoria matemática da comunicação” matematiza a informação e dá as bases para o conhecimento de transmissão de informação em computadores.

Lógica Paraconsistente: Classes

A lógica paraconsistente possui muitas classes podendo ser proposicional ou de 1ª ordem (lógica deôntica paraconsistente, lógica para inconsistência, lógica discursiva, lógica formal inconsistente, lógica paraconsistente anotada). A lógica proposicional paraconsistente anotada é subdividida em evidencial, com 2 valores (grau de crença e descrença), com 3 valores (grau de crença, descrença e especialidade), com 4 valores (grau de crença, descrença, especialidade e temporalidade), dentre outros.

Lógica Proposicional Paraconsistente Anotada com 2 valores (LPA2v)

A) Reticulado Pt

Inicialmente, fixamos um reticulado finito denominado de reticulado de valores-verdades, t = < | t |, ≤ >, então t é um reticulado se:

• ∀x, x ≤ x ( reflexividade )
• Se x ≤ y e y ≤ x => x = y ( anti-simetria )
• Se x ≤ y e y ≤ z => x ≤ z ( transitividade )
• ∀x, y ∈ | t |, existe o supremo de x e y que denotamos por x v y
• ∀x, y ∈ | t |, existe o ínfimo de x e y que denotamos por x ^ y

Associamos a este reticulado os seguintes símbolos:

• ⊥ => que indica o mínimo de t
• Τ => que indica o máximo de t

A representação de um reticulado finito se faz usualmente através do diagrama de Hasse.

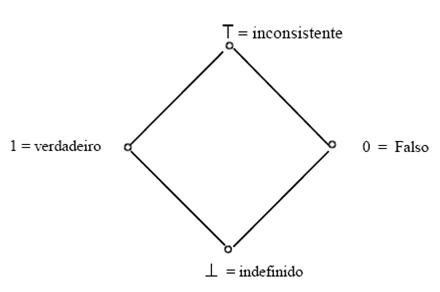Reticulado Finito

Fixamos, também, um operador ¬ | t | → | t | que terá intuitivamente o “significado” da negação da Lógica Pt. No exemplo anterior ele define-se como:

• ¬ ( 1 ) = 0
• ¬ ( 0 ) = 1
• ¬ ( T ) = T
• ¬ (⊥ ) = ⊥

B) Linguagem Pt

Lógica Paraconsistente: Definição

No mundo real, as inconsistências são importantes e não podem ser desprezadas porque são as informações contraditórias que trazem fatos relevantes modificando, às vezes, completamente o resultado da análise. A existência da inconsistência é que induz ao sistema promover buscas procurando novas e esclarecedoras informações com consultas a outros informantes, para se obter uma conclusão mais real e confiável.

Seja uma proposição que contenha a premissa: “Esta maça é vermelha”. Sob a perspectiva de lógicas clássicas só poderemos afirmar que ela é vermelha (Verdadeiro) ou não é vermelha (Falso). Entretanto, sabemos que a maçã pode possuir diversas tonalidades, variando do verde ao vermelho. A representação de tal proposição em computação binária se torna impossível, já que o modelo binário tem grandes dificuldades de tratar inconsistências, ambiguidades, paradoxos e incertezas que ocorrem com freqüência no mundo real.

A lógica paraconsistente recebe a seguinte definição, supondo que a linguagem L, subjacente a uma teoria dedutiva F, contém um símbolo para a negação. Então, F é dita ser inconsistente se e somente se possuir dois teoremas, dos quais um é a negação do outro; caso contrário, F é dita consistente. A teoria F é dita trivial se e somente se todas as fórmulas (ou todas as sentenças) da linguagem de L são teoremas de F; caso contrário diz-se que F é não-trivial. Ou seja, lógicas não triviais são aqueles que não satisfazem a seguinte teoria: “Uma teoria chama-se trivial ou supercompleta quando todas as proposições expressáveis em sua linguagem forem também teoremas”.

Outras definições importantes que completam um perfeito entendimento da lógica paraconsistente são:

Lógica Paraconsistente: Professor Newton Carneiro Afonso da Costa

Newton da Costa nasceu em 16 de setembro de 1929, na cidade de Curitiba, Estado do Paraná. Filho de Dimas Carneiro Affonso da Costa e Sylvia Carneiro Affonso da Costa aos quinze anos interessou-se por questões de Lógica e pelos Fundamentos da Matemática. Com o apoio de um de seus tios, Milton Carneiro, então professor de História da Filosofia da Faculdade de Filosofia, Ciências e Letras da Universidade Federal do Paraná, iniciou-se em filosofia por meio de diálogos de Platão e de vários textos de Aristóteles, ambos em traduções francesas. Encantado com a filosofia debruçou-se sobre as obras de autores como Descartes, Poincaré, Lalande e outros, mas foi Bertrand Russell que exerceu forte impacto sobre o jovem Newton, embora este “divirja fundamentalmente de Russell como filósofo”, no entanto admirando-o como lógico, reformador social e ensaísta-publicista.

Newton da Costa e Família

Da Costa obteve três graduações pela Universidade Federal do Paraná: em 1952, Engenharia Civil pela Escola de Engenharia, no ano de 1955 o Bacharelado em Matemática e em 1956 a Licenciatura em Matemática ambos pela Faculdade de Filosofia, Ciências e Letras. Ainda na Faculdade de Filosofia, Ciências e Letras da Universidade Federal do Paraná, no ano de 1961, Newton da Costa recebe o título de Doutor em Matemática e se torna Livre Docente de Análise Matemática e Análise Superior. Em 1964, torna-se Professor Catedrático na mesma área de sua livre-docência. O Professor Newton da Costa, já chamado por seus pares e alunos como Professor da Costa, lecionou 14 anos na Universidade Federal do Paraná.

Formatura de Newton da Costa em engenharia civil (1952)

Newton da Costa foi:

1. Diretor Associado do Instituto de Matemática, Estatística e Ciências da Computação da Unicamp em 1967;
2. Professor Titular do Instituto de Matemática, Estatística e Ciências da Computação da Unicamp de 1968-1969;
3. Professor Titular do Instituto de Matemática e Estatística da USP de 1970-1981;
4. Professor Titular do Departamento de Filosofia da Faculdade de Filosofia, Letras e Ciências Humanas da USP de 1982-1999;
5. Pesquisador do Instituto de Estudos Avançados da USP desde 1985.

Newton da Costa na conferência na Universidade de Torum, na Polônia (1976)

Lógica Paraconsistente: História

Aristóteles (384-322 a.C.) apresentou a primeira sistematização da lógica da qual se tem notícia. Não obstante alguns desenvolvimentos posteriores, pouco conhecidos até perto do início do século XX, os princípios básicos da lógica de tradição aristotélica permaneceram incólumes, sem alterações significativas, até o século XIX. O filósofo Immanuel Kant (1724-1804) chegou mesmo a dizer que, em matéria de lógica, nada mais poderia ser acrescentado ao que fez Aristóteles. A partir de meados do século XIX, no entanto, matemáticos como George Boole (1815-1864), Gottlob Frege (1848-1925) e Giuseppe Peano (1858-1932) deram contribuições significativas para a criação daquilo que ficou conhecido como lógica matemática. Por seu intermédio, a lógica tornou-se uma disciplina com características matemáticas, tendo alcançado um desenvolvimento extraordinário, com implicações as mais variadas em praticamente todos os campos do saber.

Entre 1910 e 1913, o lógico polonês Jean Lukasiewicz (1876-1956) e o lógico russo Nicolai Vasiliev (1880-1940) chamaram a atenção, de forma independente, para o fato de que, similarmente ao que se deu com os axiomas da geometria euclidiana, alguns princípios da lógica aristotélica poderiam ser revisados, inclusive o princípio da contradição. No seu célebre trabalho de 1910, sobre o princípio de contradição em Aristóteles, bem como em artigo do mesmo período, Lukasiewicz examinou três formulações distintas do princípio da não contradição (uma ontológica, uma lógica e uma psicológica), e rejeitou cada uma delas, argumentando que tal princípio não é válido sem restrições.

                                  
Jean Lukasiewicz                                                     Nicolai Vasiliev

Como consequência, criou-se um precedente para o estudo das lógicas nas quais tais leis não se encontram satisfeitas — possibilitando, dessa forma, o aparecimento de lógicas não clássicas. Contudo, como Lukasiewicz não elaborou, naquele período, qualquer tipo de sistema lógico, esse precedente, em certa medida, perdeu-se. O questionamento do quinto postulado de Euclides por Vasiliev, o postulado das paralelas, mostrou que ele era independente dos demais axiomas da geometria euclidiana, podendo ser substituído por alguma forma de negação. Isso deu origem às chamadas geometrias não-euclidiana de extrema importância inclusive em física.